MATEMÁTICAS II
 TEOREMA DE PARES DE ÁNGULOS
 Ángulos complementarios Un par de ángulos son complementarios si la suma resultante de sus medidas es 90°. Los ángulos complementarios no tienen que ser congruentes entre sí. Lejos de eso, la única cualidad que los define es que la suma de sus medidas es igual a la medida del ángulo recto: 90°

Ángulos suplementarios Dos ángulos son suplementarios si su suma es igual a 180°. Al igual que los ángulos complementarios, los ángulos suplementarios no tienen que ser congruentes entre sí, ni siquiera tienen que estar adyacentes. Su única cualidad es que al sumarlos, el resultado dé 180°

Ángulos adyacentes.Dos ángulos son adyacentes si ambos comparten el mismo vértice y un lado, pero no se traslapan. En el diagrama de abajo,  y  son adyacentes.

Ángulos conjugados. Son dos ó mas ángulos que al sumarlos su resultado es igual a 360°

TEOREMA DE RECTAS PARALELAS Y UNA SECANTE 

Consideremos un sistema de dos rectas cortadas por una secante o transversal. En este caso tenemos, para cada intersección, un sistema de dos rectas que se cortan entre si, obteniendo de esta manera varios ángulos opuestos por el vértice y adyacentes, correspondientes a cada intersección. Pero también podemos clasificar los ángulos de acuerdo a la posición que ocupan con respecto a los sistemas adyacentes.

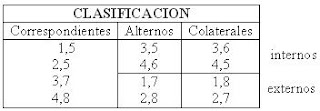
los ángulos correspondientes entre rectas paralelas y una transversal son congruentes

los ángulos alternos y internos entre rectas paralelas y una transversal son congruentes

RELACIÓN ENTRE ÁNGULOS INTERIORES Y EXTERIORES DE UN TRIANGULO

En un triángulo existen dos tipos de ángulos:

Los ángulos interiores lo forman dos lados.

Los ángulos exteriores lo forman un lado y su prolongación.

propiedades de los ángulos de triángulo

1. La suma de los ángulos interiores de un triángulo es igual a 180°.

A + B + C = 180º

2.  El valor de un ángulo exterior de un triángulo es igual a la suma 

de los dos interiores no adyacentes.

α = B + C

3.   Un ángulo interior y exterior de un triángulo son suplementarios, 

es decir, suman 180º.

α = 180º - A

TEOREMA DE CONGRUENCIA DE TRIÁNGULOS

Primer criterio: lado, lado, lado (LLL)

Dos triángulos son congruentes si los tres lados de uno de ellos son congruentes a los lados del otro triángulo.

Segundo criterio: lado, angulo, lado (LAL)

Dos triángulos son congruentes si, en el primer triangulo, dos de sus lados y el angulo comprendido entre ellos del segundo triangulo

Tercer criterio: angulo, lado, angulo (ALA)

Dos triángulos son congruentes si dos ángulos y el lado comprendido entre ellos, de uno de los triángulos, son congruentes con dos de los ángulos y el lado comprendido entre ellos del otro triangulo.

TEOREMAS DE SEMEJANZAS DE TRIÁNGULOS

Dos triángulos son semejantes si tienen dos ángulos iguales.

     

 Dos triángulos son semejantes si tienen los lados proporcionales.

     

Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.

     

EN TRIÁNGULOS RECTÁNGULOS:

Dos triángulos rectángulos son semejantes si tienen un ángulo agudo igual.

Dos triángulos rectángulos son semejantes si tienen los dos catetos proporcionales.

Dos triángulos rectángulos son semejantes si tienen proporcionales la hipotenusa y un cateto.

     

TEOREMA DE TALES

Entonces, veamos el primer Teorema de Tales en un triángulo:

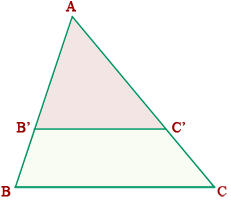Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triángulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC.  Lo que se traduce en la fórmula

Otra variante del Teorema de Tales

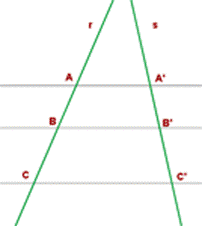Del primer teorema de Tales se deduce además lo siguiente (realmente es otra variante de dicho teorema, y, a su vez, consecuencia del mismo): Si dos rectas cuales quieras (r y s) se cortan por varias rectas paralelas (AA’, BB’, CC’) los segmentos determinados en una de las rectas (AB, BC) son proporcionales a los segmentos correspondientes en la otra (A’B’, B’C’).

TEOREMA DE PITAGORAS

En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)